GSP (Java Gezgin Satıcı Problemi)

Gezgin Satıcı Problemi veya yabancı kaynaklarda bulabileceğiniz ismi ile “Traveling Salesman Problem” Bilgisayar Bilimleri’nin gelişmesine büyük katkı sağlayan problemlerden bir tanesidir.

Çözmesi anlaması kadar kolay olmayan problemi bu yazımız da inceleyip genel bir bilgi sahibi olmaya çalışalım.
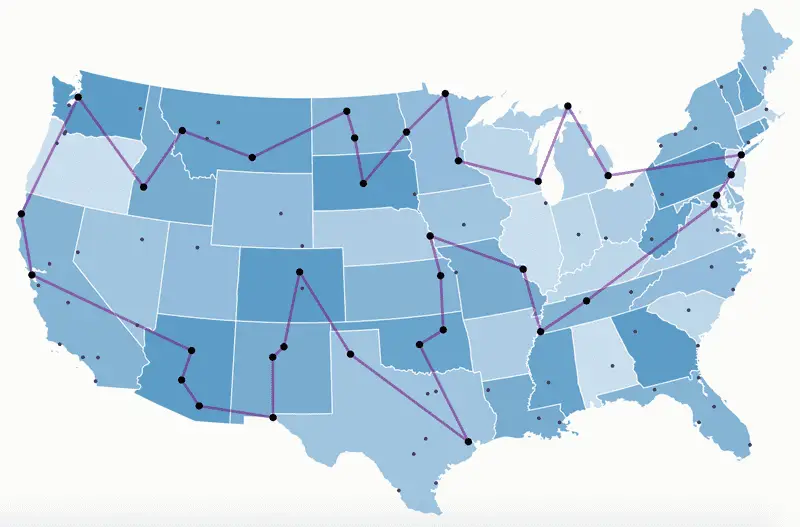
Problem de amaç, bir satıcının bulunduğu şehirden başlayarak her şehre sadece bir kez uğradıktan sonra başladığı şehre dönen en kısa turu bulmaktır.Şehirler arası gidişi kuş bakışı olarak kabul edersek aşağıdaki örnek harita ile problem tam olarak anlaşılacaktır. Verilen resimde çizilen alternatif bir yolu temsil etmektedir.

Problem, çizge kuramı dilinde, şehirlerin noktalarla, şehirler arası yolların kenarlarla temsil edildiği (yalın) bir çizge üzerinde, en kısa Hamilton turunun bulunmasıdır.

Hamilton turu, bir çizge üzerindeki her noktadan sadece bir kez geçen ve başladığı noktada biten, 19. yüzyılda yaşamış matematikçi William Hamilton’ın adıyla anılan turdur.

Örneğin n noktadan oluşan bir tam çizge, yani Kn tamçizgesi (n−1)!/2 Hamilton turu içerir.

Bu noktada problemimizi anladığımızı kabul ediyor ve bulmamız gereken turun en iyi (kısa) Hamilton turu olduğunu belirterek problemin zorluğunun anlaşılması için küçük bir hesap yapmak istiyorum.

Yöntemde izleyeceğimiz yollar şöyle:

1.  Çizgenin tüm Hamilton turlarını bul.
2.  Her turun uzunluğunu hesapla.
3.  Turlar arasından en kısasını seç.

Bu çözüm yöntemi ile, 10 şehir için gereken tur sayısı 9!/2 = 181.440’tır.

Şehir sayısı 20’ye çıktığında ise bulunması gereken tur sayısı 19!/2 ≈ 6,08 × 1016’yı bulur.

25 şehir için ise yaklaşık 3,1 × 1023 turun incelemesi gerekir.

Eğer satıcı, 25 şehirli bir GSP problemini, her Hamilton turunu 10-9 saniyede inceleme kapasitesine sahip bir bilgisayarla çözmeye kalkarsa, ancak 10 milyon yıl sonra en kısa turu bulabilir…
Satıcı Problemi

package gsp;

import java.io.BufferedReader;
import java.io.File;
import java.io.FileNotFoundException;
import java.io.FileReader;
import java.io.IOException;

public class SatýcýProblemi {
 
 public static void main(String[] args) {
  // TODO Auto-generated method stub
  File dosya=new File("sehirmesafe.txt");
  
  String [][]mesafeolcum;
  int [][] gerceldegerler;
  BufferedReader buffereader=null;
  int k=0;
  int j=0;
  try {
   buffereader=new BufferedReader(new FileReader(dosya));
   String oku=buffereader.readLine();
   while(oku!=null){
    oku=buffereader.readLine();
    k++;
   }
   String[]sehirlerarasimesafe=new String[k];
   buffereader=new BufferedReader(new FileReader(dosya));
    oku=buffereader.readLine();
   while(oku!=null){
    sehirlerarasimesafe[j]=oku;
    oku=buffereader.readLine();
    j++;
    
   }
   for(int i=0;i<sehirlerarasimesafe.length;i++){
    System.out.println(sehirlerarasimesafe[i]);
   }
   
   mesafeolcum=new String[sehirlerarasimesafe.length][];
   for(int a=0;a<sehirlerarasimesafe.length;a++){
    mesafeolcum[a]=sehirlerarasimesafe[a].split(",");
   }
   gerceldegerler=new int[sehirlerarasimesafe.length][mesafeolcum[0].length];
   for(int e=0;e<sehirlerarasimesafe.length;e++){
    for(int l=0;l<mesafeolcum[0].length;l++){
     System.out.print(mesafeolcum[e][l]+"\t");
     gerceldegerler[e][l]=Integer.parseInt(mesafeolcum[e][l]);
    }
    System.out.println();
   }
    for (int i = 0; i <sehirlerarasimesafe.length; i++)
             {
                 for (int t= 0; t < mesafeolcum[0].length; t++)
                 {
                    if (gerceldegerler[i][t] == 1 && gerceldegerler[t][i] == 0)
                     {
                         gerceldegerler[t][i] = 1;
                     }
                 }
                 
             }
    System.out.println("Gezilen sehirler sýrasýyla:");
             Sehirlerarasý gezmeislemi = new Sehirlerarasý();
             gezmeislemi.Gezme(gerceldegerler);
    
   
  } catch (FileNotFoundException e) {
   // TODO Auto-generated catch block
   e.printStackTrace();
   System.out.println("Dosyayý acma hatasý..");
  } catch (IOException e) {
   // TODO Auto-generated catch block
   e.printStackTrace();
   System.out.println("Dosya okuma hatasý");
  }
  
 }

}

Şehirler Arası mesafe

package gsp;

import java.util.Stack;

public class Sehirlerarasý {
 private int sehirnumaralarý;
 private Stack<integer> stack;
 
 public Sehirlerarasý(){
  stack=new Stack<integer>();
 }
 public void Gezme(int mesafe[][]){
  sehirnumaralarý=mesafe[0].length-1;//Burada kendi þehrimiz haric sehirleri belirledik
  int [] gezilensehir=new int[sehirnumaralarý+1];//Burada sehir gezilen listesi olusturduk
  gezilensehir[1]=1;
  stack.push(1);//Butun stacklere 1 degerini atadýk.
  int deger,dst=0,i;
  int mindeger=Integer.MAX_VALUE;
  boolean mingitme=false;
  System.out.println(1+"\t");
  while(!stack.isEmpty())
  {
   deger=stack.peek();
   i=1;
   mindeger=Integer.MAX_VALUE;
   while(i<=sehirnumaralarý){
    if(mesafe[deger][i]>1 &&gezilensehir[i]==0){
     if(mindeger>mesafe[deger][i]){
      mindeger=mesafe[deger][i];
      dst=i;
      mingitme=true;
     }
    }
    i++;
   }
   if(mingitme){
    gezilensehir[dst]=1;
    stack.push(dst);
    System.out.println(dst+"\t");
    mingitme=false;
    continue;
   }
   stack.pop();
  }
 }
}

Şehirler arası mesafe text dosyası

000,374,200,223,108,178,252,285,240,356
374,000,255,166,433,199,135,095,136,017
200,255,000,128,277,128,180,160,131,247
223,166,128,000,430,047,052,084,040,155
108,433,277,430,000,453,478,344,389,423
178,199,128,047,453,000,091,110,064,181
252,135,180,052,478,091,000,114,083,117
285,095,160,084,344,110,114,000,047,078
240,136,131,040,389,064,083,047,000,118
356,017,247,155,423,181,117,078,118,000