C Programlama DFS Algoritması (Depth-first Search)

Bu dersimizde ise Graph Teorisi’nin temel gezme algoritmalarından olan DFS Algoritmasından bahsedeceğiz.

Graph’ı gezmek ne demek?

Elimizde bir graph olduğunu düşünelim. Bunun gösterimi komşuluk matrisi veya komşuluk listesi şeklinde olabilir. Bizim amacımız graph‘ın sahip olduğu edge‘leri (yolları) kullanarak her bir node‘un yalnızca bağlı olduğu node’lara gitmesine olanak sağlamak. Somut bir örnek vermek gerekirse, graph’ı bir ülke node’ları da birer şehir olarak düşünelim. Malesef bu ülkede herhangi bir şehirden bütün şehirlere direkt yol bulunmamakta. Bu durumda yalnızca mevcut yolları kullanarak gideceğimiz şehire uygun bir path  belirlemeliyiz.

Amacımız spesifik olarak A şehrinden B şehrine gitmek zorunda olmayabilir. Bütün şehirleri de gezmek için bu algoritmalara ihtiyacımız var.

DFS (Depth-first Search) Algoritması

Türkçesi “Derinlik öncelikli arama” şeklinde geçen DFS algoritması bizim belirlediğimiz bir root (kök) node’dan başlıyor ve herhangi bir çocuğunu seçiyor. Daha sonra bu çocuktan daha önce gezmediğimiz herhangi bir node’a gidiliyor. Bu seçimlerdeki iki kuralımız var birincisi seçeceğimiz node’a direkt yol olmalı diğeri ise o node daha önce gezilmemiş olmalı. Bu kuralları uygulayarak rekürsif bir şekilde geziliyor.

Ancak öyle bir node’a geliyoruz ki gidilecek yer kalmıyor. Çünkü direkt bağlantımızın olduğu bütün node’lar daha önceden gezilmiş. Böyle bir durumda ise bu node’dan önce en son gezdiğimiz node’a geri dönüyoruz ve başka tercihler var mı diye bakıyoruz. Algoritma rekürsif olarak çalıştığı için her takıldığımız noktada bir üste çıkmamıza olanak sağlıyor. Algoritmamız başladığımız yere geldiğimizde ve hali hazırda bütün çocuklarımızı gezdiğimizde bitiyor.

Biraz karışık gibi gözükebilir farkındayım ancak biraz sonra vereceğim somut örnekle anlaşılacağını düşünüyorum.

DFS Örneği

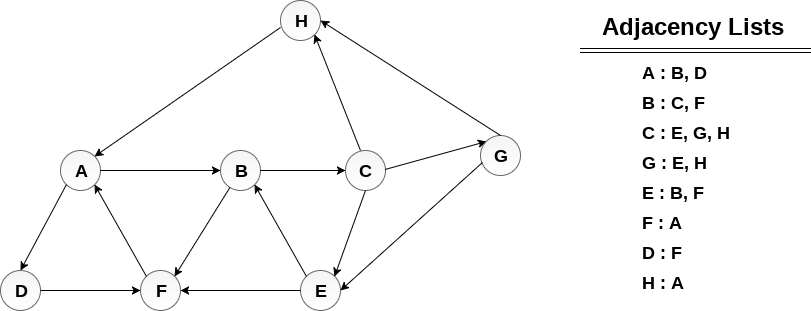
Şimdi beraber yukarıdaki graph’ta örnek bir DFS algoritması uygulayalım.

Öncelikle root olarak B seçelim.  B’nin herhangi bir çocuğundan başlamamız lazım. A seçelim. A’dan daha önce gezmediğimiz ve direkt yol olan node’lar D ve E. Bunlardan rastgele E seçelim. E’den C, F ve D node’larına gidebiliyoruz. D seçelim. Şimdi D’ye geldiğimizde fark ediyoruz ki gidecek başka bir yer kalmadı çünkü A ve E’yi halihazırda gezmiştik. Algoritmaya göre tıkandığımız node’dan bir önceki node’a yani E’ye gitmemiz gerek. E’ye geri döndükten sonra F’yi seçelim. Buradan da C’yi seçmek zorundayız. Şu an C’deyiz ve gezilmemiş herhangi bir node kalmadı. Algoritmaya göre bir önceki adıma gidip başka bir alternatifim var mı onu kontrol ediyoruz. Ancak C’den önce gittiğimiz F’de de gezilmedik node kalmamış. Rekürsif olarak ilerleyen fonksiyonumuz başlangıçtan beri bütün node’ları kontrol ediyor ancak gezilmemiş node kalmadığı için en son başlangıç noktamız olan B’yi de kontrol edip bitiriyor.

Buna göre DFS sıralamamız B – A – E – D – F – C şeklinde oldu. Rastgele yaptığımız seçimleri değiştirdiğimizde bazı node’ların yeri oynayacaktır ancak bize verilen yolların dışına çıkılmamış olacaktır.

DFS’in Karmaşıklığı:

Algoritmanın iki temel kuralından birisi olan daha önce gezilmiş bir node’a tekrar gidilmemeli kuralına göre her node tam olarak 1 kez geziliyor. Node sayısını N ile temsil edersek karmaşıklık O(N) oluyor.

C Programlama Örneği

#include<stdio.h>
#include<conio.h>
#include<stdlib.h>
int a[20][20],reach[20],n;
void dfs(int v)
{
 int i;
 reach[v]=1;
 for(i=1;i<=n;i++)
  if(a[v][i] && !reach[i])
  {
   printf("\n %d->%d",v,i);
   dfs(i);
  }
}
int main()
{
 int i,j,count=0;
 system("CLS");
 printf("\n Enter number of vertices:");
 scanf("%d",&n);
 for(i=1;i<=n;i++)
 {
  reach[i]=0;
  for(j=1;j<=n;j++)
   a[i][j]=0;
 }
 printf("\n Enter the adjacency matrix:\n");
 for(i=1;i<=n;i++)
  for(j=1;j<=n;j++)
   scanf("%d",&a[i][j]);
 dfs(1);
 printf("\n");
 for(i=1;i<=n;i++)
 {
  if(reach[i])
   count++;
 }
 if(count==n)
  printf("\n Graph is connected");
 else
  printf("\n Graph is not connected");
 getch();
 return 0;
 
}

BFS Algoritması dersine buradan gidebilirsiniz.